
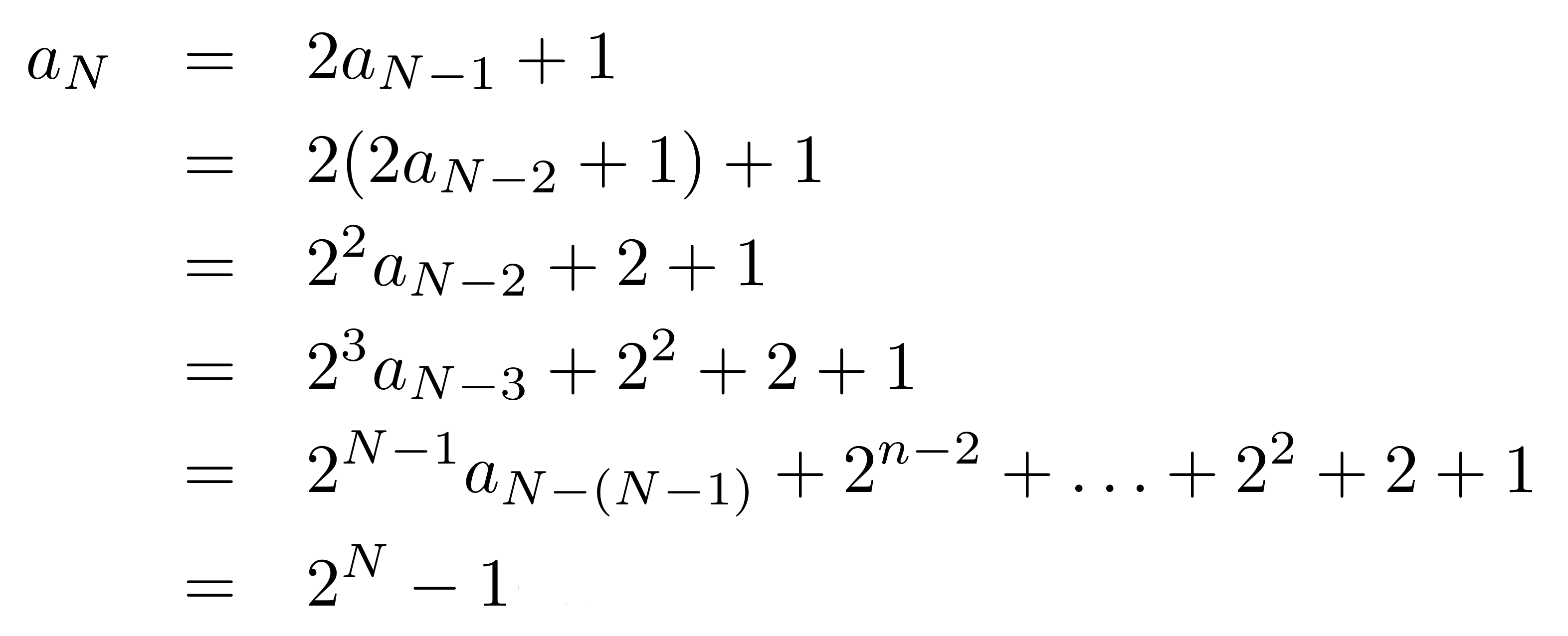
#Hanoi towers speed code#
Normally animation code can utilize JavaScript timer functions: setInterval() or setTimer(). Animation Handling in JavaScript is Problematic The above algorithm encodes the preceding description but with the parameters for the towers kept as variables instead of being specific values. After this, we can move the n-th disk from tower #0 to tower #2 and then move all the n-1 disks from the middle tower to the last tower using tower #0 as intermediate by the call Hanoi(n-1, 1,2,0). This moves the disks to the middle tower (#1) using the other tower (#2) as intermediate. The recursive algorithm for the tower of Hanoi is based on observing that the top n-1 disks at the "from" tower (together with the other two towers) represent a smaller-size instance of the original problem and, thus, can be solved by the call Hanoi(n-1, 0,1,2). Then express the solution for the original problem in terms of the solutions to the subproblems. Normally (if we denote the towers with 0,1,2), the initial call for n disks will be Hanoi(n,0,2,1).Ī recursive algorithm normally tries to find subproblems (instances of the original problem but with smaller problem size). via: the "via" tower is that used as an intermediate location as disks are moved between the towers from and to.to: the "to" tower is where the disks must be finally placed.from: the "from" tower is where the disks are placed.n: number of disks serves as the problem size for recursion.The input to the algorithm are 4 integer parameters, as follows: All Rights Reserved Worldwide.// callStack.push() // save parameters to callStack array If you copy/modify/improve the code, I would appreciate an acknowledgment This version is free, and can be downloaded locally and mirrored in its entirety. Updated syntax via JSLint and tested with newer browsers The iterative version (which more easily supports Stop) is based on some Scheme code The "classical" version uses a recursive algorithm I saw an InterLisp-D version of Tower of Hanoi in late 70s at Xerox PARC. You can watch the program do this by setting method to Move and Speed to Slow. Here are step-by-step directions for 3 disks (#1 refers to smallest disk)
#Hanoi towers speed how to#
If you knew how to move the top 2 disks somewhere else, e.g.,Īll you would have to do then is move the bottom disk to the right Īnd since you already know how to move 2 disks, With the situation of 3 disks starting on left stack: (even though the actual underlying algorithm is implemented Remember, you cannot place a larger disk on top of a smaller one (unless you "cheat") jump program moves disks quickly* between stacks (see "Speed") move program moves disks between stacks in more steps cheat like user, but you can place any disk on top of another one Example Then click on destination stack or use use buttons at bottom. To move a disk in newer browsers, click on source stack (button at bottom may highlight), Method user (default): move a disk between stacks 0-2 until you solve (or get tired) Note: if you have image loading disabled, you will have to do an explicit Load/Show Images Start/Stopįor jump and move methods, this starts solving for MSIE, button changes to Stop. Use Hanoi Movesīased on n Disks, total expected moves until solution: 2 n-1 Movesĭisplays the current number of moves Speed Slow 0.5 seconds (500ms) between each jump or move step Medium 0.1 seconds (100ms) Fast 0.01 seconds (10ms) DisksĬhoose a number (2-14) based upon selected Speed and your patience. So you must move disks temporarily to another stack. However, you cannot place a larger disk on top of a smaller one, You must move these to another stack (on the right) one at a time. In the classic "Tower of Hanoi" game/puzzle,Ī stack of disks, sorted by size, appears (on the left). Let me know about your experience with other browsers. If Images are not loaded automatically, you'll have to Load/Show Images manually after (re)loading page. On 2.x Newton with i:General:NewtonScript:Compile preference) īesides Newt's Cape, it has been tested with

Hanoi requires a browser with JavaScript support


 0 kommentar(er)
0 kommentar(er)
